(s, # w [#]) |-* (h, # Y [#]) for w in L and
(s, # w [#]) |-* (h, # N [#]) for w not in L.
Suppose you have three TM's M1, M2, and M3 that respectively decide the three languages L1, L2, and L3 that are defined over the alphabet {a,b}. Give the machine schema for a TM M that decides the language L= { w in {a,b}* : w is in at least two of the languages L1, L2 or L3}. You can use a copy machine C in your machine schema. The copy machine C when started with (s, # w [#]) for a string w over {a,b} halts with (h, # w # w [#]).
(a) [5] Design a TM M that has alphabet {#, a, b} and four states {s, t, u, v} that takes AS MANY STEPS AS POSSIBLE before an observer watching the computation of M on input bab who can see the steps of the computation but not the description of your TM (and does not know the number of states/symbols it has) can conclude that the TM is never going to move its head to the left. Hand in the output you get from running the TM simulator on your TM edited to stop at the point where the observer can tell that the TM is not going to ever move its head to the left. Explain why it is obvious that the TM M will never move its head to the left at that point.
If you save your TM in q2.txt, to make output to print, run the
TM simulator like this:
javac *.java
java TM < q2.txt > oq2.txt
The TM simulator has infinite loop protection in it
to ensure that it will not continue computing forever.
If you do not want to lose marks for this question,
make sure that you EDIT oq2.txt before printing it
to eliminate the steps that occur after the observer
can conclude that the TM never moves its head to the left.
(b)
[5]
The TM simulator starts numbering the initial configuration
with Step 0. For example, with start state s and input bab, it starts with:
Step 0 : (s, #bab[#])
For an arbitrary TM M and input string w,
what is the maximum Step Number that the TM simulator would
have to print before you
you can determine from watching the steps of
the computation of M on input w either that it
moves its head to the left or that it never will?
Express your answer as a function of k (the number of states
of the TM M) and s (the number of tape symbols in M's alphabet).
Justify your answer.
(c)
[5]
Consider the following question:
Given a TM M, and input w,
does M ever move its head to the left when started
in a configuration (s, # w [#]),
where s is the start state of M?
How could you modify my TM simulator program to turn it into
a program that can decide the answer to this question?
Hint: Use your answer to (b).
Run M1 on aa and if it halts then halt with the answer yes. Otherwise, run M2 on input aa
(a) [3] Provide the machine schema for two specific TM's M1 and M2 such that this approach will prove ineffective.
(b) [3] How can you modify the student answer to provide a correct solution to the final exam question?
(c) [4] What could you do to design a TM that halts if and only if there is some string over {a}* such that both M1 and M2 halt on this string?
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| L | R | # | ( | ) | q | a | 0 | 1 | , |
The string "M" is:
(q01, a0010, q01, a0000), (q01, a0100, q01, a0000), (q01, a0101, q00, a0101), (q01, a0111, q01, a0000), (q01, a1000, q10, a0001), (q10, a0111, q10, a0000), (q10, a1000, q10, a0001), (q10, a0101, q00, a1000)
(a) [4] What is M?
Start state of M:
| State | Symbol | Next state | Head Instruction |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
| ______ | ______ | ___________ | _________________ |
(b) [6] Is the question:
Does M from part (a) halt on input "M"?
decidable or not? You can assume that the problem:
Given M, does M halt when started on a blank tape?
is not decidable in formulating your answer.
Problem P1: Given a TM M, does M halt on every input string w in {a,b}* that has length 3 or less?
Problem P2: Given a TM M, does M halt on input string abaab?
(a)
[10]
Prove that if you have an algorithm for problem P1 then you
can design an algorithm that finds the answer to problem P2.
(b)
[5]
Which one of these statements does your answer to (a) prove:
S1: If P1 is not decidable them P2 is not decidable.
S2: If P2 is not decidable them P1 is not decidable.
Justify your answer (hint: the correct proof is a proof by contradiction).
(a) [4] Describe in terms of the input and output the (hard) variant of this optimization problem which is in NP.
Input:
Output:
(b) [3] Describe precisely a certificate for this problem that could be typed in as input using only integer values.
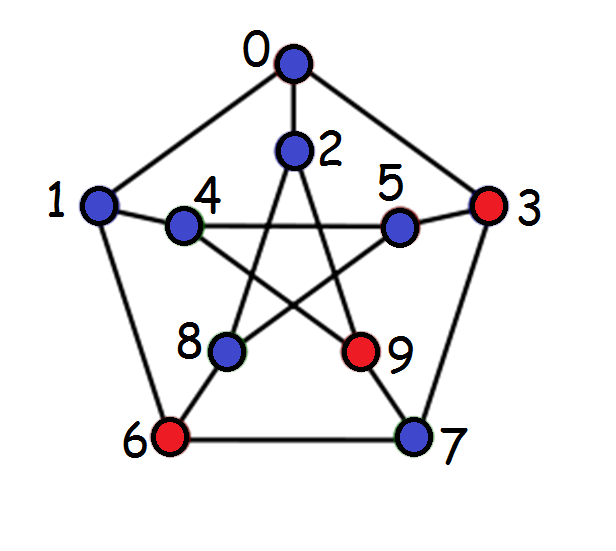
(c) [2] Show what you would type in as a certificate for the dominating set (the red vertices) for this graph:
(d)
[3]
Give detailed pseudocode for
an efficient algorithm for reading in your certificate and checking
if it is valid.
Assume that the graph G is already stored using an adjacency list
representation.
(e)
[3]
Provide a tight analysis of the time complexity
(use THETA notation) for your
approach from (d) for the case that the input graph
is stored in an adjacency list representation.
Justify your answer by annotating your algorithm from (d)
to indicate the time complexity of each step of your
certificate checking algorithm.
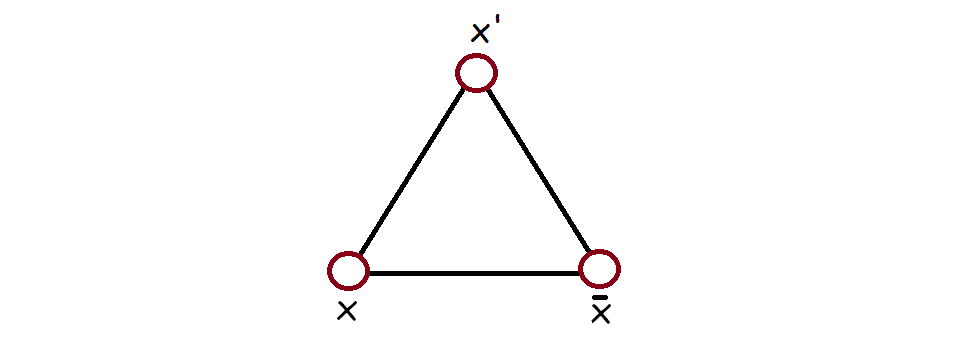
For each clause, there is a vertex of the graph connected to the three literals in the clause. If the 3-SAT problem has k variables and c clauses then this constructed graph has 3k+c vertices and 3k+3c edges.
(a) [3] Draw the graph that arises from this 3-SAT system:
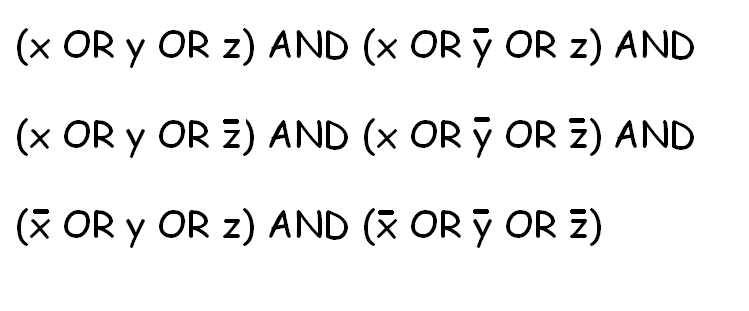
(b) [3] Find a satisfying assignment of this 3-SAT system and show a corresponding dominating set on the graph.
(c) [4] For a general problem, if the 3-SAT system has a satisfying truth assignment, what size dominating set can you find?
(d) [5] Prove that it is not possible to find a dominating set of the size you specified for part (c) when the 3-SAT system has no satisfying truth assignments.
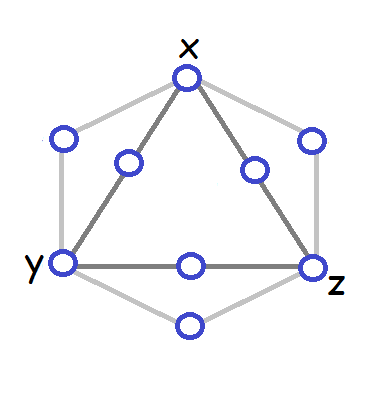
where the variables x, y, and z in the clause gadget are connected to
the corresponding triangle vertices as per the previous question.
(a) [5] What is the minimum size of a dominating set that the resulting graph
will have when
the 3-SAT problem is solvable and what will a minimum dominating set
look like?
Justify your answer.
(b) [5] Prove that if the 3-SAT problem has no solutions then the
graph does not have a dominating set of the size you indicated for
part (a).